Lösungen Band II, Vorlesung 4

Aufgabe 4.1

Beweisen Sie: Ist \textbf{U} unitär, und sind \ket{A} und \ket{B} zwei beliebige Zustandsvektoren, so ist das innere Produkt von \textbf{U}\ket{A} und \textbf{U}\ket{B} dasselbe wie das innere Produkt von \ket{A} und \ket{B}. Man könnte dies die Erhaltung der Überlappungen nennen. Tatsächlich drückt es die Tatsache aus, dass die logische Beziehung zwischen Zuständen mit der Zeit erhalten bleibt.

Lösung:

Ist \op{U} unitär, so gilt \op{U}^\dagger\op{U} = \Id und damit \bra{A}\op{U}^\dagger \op{U} \ket{B} = \bra{A}\Id\ket{B} =\braket{A|B}.

Aufgabe 4.2

Beweisen Sie, dass für hermitesche \textbf{M} und \textbf{L} auch i[\textbf{M},\textbf{L}] hermitesch ist. Beachten Sie, dass das i wichtig ist. Der Kommutator für sich allein ist nicht hermitesch.

Lösung:

Wir fangen einfach mal an zu rechnen und verwenden die Definition des Kommutators:

    \[ [\op{M},\op{L}]^\dagger = (\op{M}\op{L} - \op{L}\op{M})^\dagger = (\op{M}\op{L})^\dagger - (\op{L}\op{M})^\dagger. \]

Die letzte Gleichung sehen wir, wenn wir mit den Komponenten der Operator-Matrizen arbeiten. Wir wissen, dass die hermitesch konjugierte Matrix durch Transponieren und komplexe Konjugation gebildet wird, d.h. die Komponenten der hermitesch konjugierten Matrix A^\dagger zu A = (a_{ij})lauten a_{ij}^*. Für zwei beliebige Matrizen A und B und deren Produkt C=A+B gilt dann

    \[ c_{ij}^\dagger = c_{ji}^* = (a_{ji} + b_{ji})^* = a_{ji}^* + b_{ji}^* = a^\dagger_{ij} + b_{ij}^\dagger,\]

also C^\dagger = (A+B)^\dagger = A^\dagger + B^\dagger. Weiterhin gilt für eine komplexe Zahl z:

    \[(zA)^\dagger = z^*A^\dagger,\]

denn es ist (z a_{ij})^\dagger = z^* a_{ji}^*. Die Bildung der hermitesch Konjugierten ist also eine lineare Operation.

Was sind nun (\op{M}\op{L})^\dagger und (\op{L}\op{M})^\dagger? Wir vermuten für zwei Matrizen A und B, dass gilt:

    \[(AB)^\dagger = B^\dagger A^\dagger.\]

Die Reihenfolge der Operatoren wird also vertauscht (man beachte, dass die Matrizenmultiplikation nicht kommutativ ist – sonst wäre der Kommutator ja sinnlos). Wir zeigen dies wieder über die Komponenten. Ist C=AB, so gilt

    \[ c_{ij}^\dagger = c_{ji}^* = ( \sum_k (a_{jk} b_{ki}))^* = \sum_k (a_{jk}^* b_{ki}^* ) = \sum_k ( b_{ki}^* a_{jk}^* ) = \sum_k ( b^\dagger_{ik} a_{kj}^\dagger ). \]

Es gilt also C^\dagger = B^\dagger A^\dagger. Damit kommen wir schon weiter:

    \[ [\op{M},\op{L}]^\dagger = (\op{M}\op{L})^\dagger - (\op{L}\op{M})^\dagger = \op{L}^\dagger \op{M}^\dagger - \op{M}^\dagger \op{L}^\dagger = \op{L}\op{M} - \op{M}\op{L} = [\op{L},\op{M}] = - [\op{M},\op{L}], \]

denn nach Annahme ist \op{L}^\dagger = \op{L} und \op{M}^\dagger =\op{M}.Der Kommutator [\op{M},\op{L}] ist also nicht hermitesch, denn die hermitesch Konjugierte hat ein negatives Vorzeichen. Der Kommutator ist antihermitesch (wenn er nicht gleich 0 und damit langweilig ist). Die Behauptung war aber, dass i[\op{M},\op{L}] hermitesch ist, und das ist nun einfach zu zeigen:

    \[ (i\op{M},\op{L}])^\dagger = i^* [\op{M},\op{L}]^\dagger = (-i ) (-[\op{M},\op{L}]) = i[\op{M},\op{L}].\]

Aus einem antihermiteschen Operator macht man durch Multiplikation mit i einen hermiteschen Operator. Wir werden das in Vorlesung 8 noch verwenden.

Aufgabe 4.3

Gehen Sie zurück zu den Poisson-Klammern aus Band I und überprüfen Sie, ob die Identifikation in Gl. 4.21 von der Dimension her konsistent ist. Zeigen Sie, dass dies ohne den Faktor \hbar nicht der Fall wäre.

Lösung:

Gl. 4.21 besagt [\op{F},\op{G}] \Longleftrightarrow i\hbar\{F,G\}, wobei die Poisson-Klammer in Band I in Gl. 9.9 definiert wurde als

    \[ {F,G } = \pd{F}{q}\pd{G}{p} - \pd{F}{p}\pd{G}{q}. \]

Der Ort q hat die Dimension einer Länge, also hat \frac{1}{\partial q} die Einheit \frac{1}{m}.

Der Impuls p hat die Dimension Masse mal Geschwindigkeit, also hat \frac{1}{\partial p} die Einheit \frac{1}{kg \frac{m}{s}} = \frac{s}{kg m}.

Zusammen ergibt sich \frac{1}{\partial q} \frac{1}{\partial p} = \frac{s}{kg m^2}, und dies wird durch die Dimension von \hbar – Energie mal Zeit – gerade aufgehoben, denn \hbar hat die Einheit \frac{kg m^2}{s}.

Aufgabe 4.4

Überprüfen Sie die Kommutator-Beziehungen der Gleichungen 4.26.

Lösung:

Wir müssen drei Kommutatoren berechnen:

    \begin{align*}[ \sigma_x,\sigma_y] &= \begin{pmatrix} 0&1\\1&0\end{pmatrix}\begin{pmatrix} 0&-i\\i&0\end{pmatrix} - \begin{pmatrix} 0&-i\\i&0\end{pmatrix}\begin{pmatrix} 0&1\\1&0\end{pmatrix} = \begin{pmatrix}i&0\\0&-i\end{pmatrix} - \begin{pmatrix}-i&0\\0&i\end{pmatrix}\\&= \begin{pmatrix}2i&0\\0&-2i\end{pmatrix} = 2i \begin{pmatrix}1&0\\0&-1\end{pmatrix} = 2i\sigma_z\\ [\sigma_y,\sigma_z] &= \begin{pmatrix} 0&-i\\i&0\end{pmatrix}\begin{pmatrix} 1&-0\\0&-1\end{pmatrix} - \begin{pmatrix} 1&0\\0&-1\end{pmatrix}\begin{pmatrix} 0&-i\\i&0\end{pmatrix} = \begin{pmatrix}0&i\\i&0\end{pmatrix} - \begin{pmatrix}0&-i\\-i&0\end{pmatrix}\\&= \begin{pmatrix}0&2i\\2i&0\end{pmatrix} = 2i \begin{pmatrix}0&1\\1&0\end{pmatrix} = 2i\sigma_x,\end{align*}

    \begin{align*}[ \sigma_z,\sigma_x] &= \begin{pmatrix} 1&0\\0&-1\end{pmatrix}\begin{pmatrix} 0&1\\1&0\end{pmatrix} - \begin{pmatrix} 0&1\\1&0\end{pmatrix}\begin{pmatrix} 1&0\\0&-1\end{pmatrix} = \begin{pmatrix}0&1\\-1&0\end{pmatrix} - \begin{pmatrix}0&1\\-1&0\end{pmatrix}\\&= \begin{pmatrix}0&2\\-2&0\end{pmatrix} = 2i \begin{pmatrix}0&-i\\i&0\end{pmatrix} = 2i\sigma_y.\end{align*}

Aufgabe 4.5

Nehmen Sie einen beliebigen 3-Vektor \vec{n} und bilden Sie den Operator

    \[ \Ham = \frac{\hbar \omega}{2} \vec{\sigma} \cdot \vec{n}. \]


Finden Sie die Energieeigenwerte und Energieeigenvektoren, indem Sie die zeitunabhängige Schrödingergleichung lösen. Erinnern Sie sich, dass Gl. 3.23 \vec{\sigma} \cdot \vec{n} in Komponentenform angibt.

Lösung:

Wir haben uns in Aufgabe 3.4 schon mit den Eigenwerten und Eigenvektoren der Observablen \sigma_n beschäftigt. Für den daraus gebildeten Hamilton-Operator gilt


    \[ \Ham = \frac{\omega \hbar}{2} \vec{\sigma} \cdot \vec{n} = \frac{\omega \hbar}{2} \begin{pmatrix} n_z& (n_x - n_y) \ (n_x+in_y)& -n_z\end{pmatrix}.\]

Die Eigenwerte von \sigma_n lauten +1 und -1, daher sind die Energieeigenwerte


    \[ E_1 = +\frac{\omega \hbar}{2} \;\;\;\text{und}\;\;\;E_2=-\frac{\omega \hbar}{2}. \]

Die zeitunabhängige Schrödingergleichung lautet also \frac{\omega \hbar}{2} \sigma_n \ket{E_{1,2}} = \pm \frac{\omega \hbar}{2}\ket{E_{1,2}} und damit


    \[ \sigma_n \ket{E_{1,2}} = \pm \ket{E_{1,2}}.\]

Aufgabe 4.6

Bereiten Sie gemäß Rezept ein Schrödinger-Ketzchen für einen einzelnen Spin zu. Die Hamilton-Funktion ist \Ham = \frac{\omega \hbar}{2} \sigma_z, die Observable \sigma_x. Der Anfangszustand ist gegeben als \ket{u} (der Zustand mit \sigma_z = +1).

Nach der Zeit t wird ein Experiment durchgeführt, um \sigma_y zu messen. Was sind die möglichen Ergebnisse, und wie lauten ihre Wahrscheinlichkeiten?


Herzlichen Glückwunsch! Sie haben nun ein echtes quantenmechanisches Problem für ein Experiment gelöst, das tatsächlich im Labor durchgeführt werden kann. Sie dürfen sich gerne auf die Schulter klopfen.

Lösung:

  1. Unser Hamilton-Operator ist

        \[ \Ham = \frac{\omega \hbar}{2} \sigma_z = \frac{\omega \hbar}{2 } \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \]


2. \ket{\Psi(0)} = \ket{u} = \begin{pmatrix} 1 \\ 0\end{pmatrix}.

3. Wir kennen die Eigenwerte und Eigenvektoren von \sigma_z; die Eigenwerte sind +1 und -1. Entsprechend sind die Energieeigenwerte von \Ham:

    \[ E_1 = +\frac{\omega \hbar}{2 }\;\;\; \text{und}\;\;\; E_2 = -\frac{\omega \hbar}{2 }. \]



Die Eigenvektoren sind dieselben wie bei \sigma_z:

    \[ \ket{E_1} = \ket{u} = \begin{pmatrix} 1 \\ 0\end{pmatrix} \;\;\;\text{und}\;\;\;\ket{E_2} = \ket{d} = \begin{pmatrix} 0 \\ 1\end{pmatrix}. \]



4. \alpha_1(0) = \braket{E_1|\Psi(0)} = \braket{u|u} = 1 \;\;\;\text{und}\;\;\; \alpha_2(0) = \braket{E_2|\Psi(0)} = \braket{d|u} = 0.


5. \ket{\Psi(0)} = \ket{u} = \sum_j \alpha_j(0)\ket{E_j} = 1 \ket{u} + 0 \ket{d}.

6. \ket{\Psi(t)} = \ket{u} = \sum_j \alpha_j(t)\ket{E_j} = \alpha_1(t) \ket{u} + \alpha_2(t) \ket{d}.


7. Wir ersetzen

    \begin{align*} \alpha_1(t) &= \alpha_1(0) e^{-\frac{i}{\hbar}E_1 t} = e^{-\frac{i}{2 }\omega t} \ \alpha_2(t) &= \alpha_2(0) e^{-\frac{i}{\hbar}E_2 t} = 0. \end{align*}


Es ist also:

    \[ \ket{\Psi(t)} = \sum_j \alpha_j(0) e^{-\frac{i}{\hbar} E_j t} \ket{E_j} = e^{-\frac{i}{2 }\omega t} \ket{u} = \begin{pmatrix} e^{-\frac{i}{2 }\omega t} \\ 0 \end{pmatrix}. \]

8. Salzen und pfeffern…

Wie wir sehen, besteht die einzige Veränderung des Startvektors \ket{u} in der Multiplikation mit einem Phasenfaktor.


Nehmen wir eine Messung des Spins in y-Richtung vor, so werden wir mit gleicher Wahrscheinlichkeit ein Ergebnis in Richtung in oder in Richtung out erhalten. Wir können dies auch nachrechnen. Die Eigenwerte des Operators \sigma_y sind +1 und -1 mit den Eigenvektoren

    \[\ket{i} =\begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} \end{pmatrix} \;\;\; \text{und}\;\;\;\ket{o} =\begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{-i}{\sqrt{2}} \end{pmatrix}. \]

Die Wahrscheinlichkeiten ergeben sich aus

    \begin{align*} \braket{i|\Psi(t)} = e^{-\frac{i}{2} \omega t} \braket{i|u} = \frac{1}{\sqrt{2}} e^{-\frac{i}{2}\omega t} &\Longrightarrow P(+1) = \frac{1}{\sqrt{2}} e^{-\frac{i}{2 }\omega t} \frac{1}{\sqrt{2}} e^{\frac{i}{2 }\omega t} = \frac{1}{2}\\ \braket{o|\Psi(t)} = e^{-\frac{i}{2} \omega t} \braket{o|u} = \frac{1}{\sqrt{2}} e^{-\frac{i}{2}\omega t} &\Longrightarrow P(-1) = \frac{1}{\sqrt{2}} e^{-\frac{i}{2}\omega t} \frac{1}{\sqrt{2}} e^{\frac{i}{2}\omega t} = \frac{1}{2}. \end{align*}

2 Kommentare

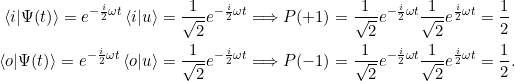
  1. Gutes Neues Jahr Herr Sippel,
    ich lese mit großer Begeisterung das Buch und versuche mich laienhaft an den Aufgaben. In Aufgabe 4.6 unter Punkt 7 wird die Zeitentwicklung für |E_1> wie folgt angegeben: exp(-i/2 * omega * t).
    Der Eigenwert E_1 wird jedoch mit E_1 = h/(2 omega) angegeben. Müßte der Eigenwert E_1 zum Hamiltonoperator (omega * h)/2 sigma_z nicht vielmehr E_1 = (omega * h)/2 lauten?
    Viele Grüße,
    Thomas Keller

    Antworten

  2. Hallo,

    und auch ein schönes neues Jahr von meiner Seite!

    Sie haben völlig recht. sigma_z hat die Eigenwerte +1 und -1. Das ist sofort zu sehen, da sigma_z Diagonalgestalt hat, und bei solchen Matrizen stehen die Eigenwerte auf der Diagobalen. Daher sind die Eigenwerte von omega h / 2 natürlich +- omega h / 2. Ich hatte die Hamilton-Funktion falsch hingeschrieben; der Fehler ist jetzt korrigiert. Vielen Dank für den Hinweis, da waren Sie aufmerksamer als ich!

    Antworten

Hinterlasse einen Kommentar.

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert