Aufgabe 1.1
Zeigen Sie, dass die ![]() -Koordinate des Punkts
-Koordinate des Punkts ![]() in Abb. 1.6 gleich
in Abb. 1.6 gleich ![]() ist.
ist.
Lösung:

Dem Bild entnehmen wir, dass der Punkt ![]() der Schnittpunkt der Geraden
der Schnittpunkt der Geraden ![]() mit der Geraden
mit der Geraden ![]() ist. Dies setzen wir in die Lorentz-Tranformation für
ist. Dies setzen wir in die Lorentz-Tranformation für ![]() ein und erhalten
ein und erhalten
![]()
also
![]()
Aufgabe 1.2
In Abb. 1.8 kehrt der reisende Zwilling nicht nur die Richtung um, sondern wechselt dabei auch in ein anderes Bezugssystem.
a) Verwenden Sie die Lorentz-Transformation, um zu zeigen, dass vor der Umkehr die Beziehung zwischen den Zwillingen tatsächlich symmetrisch ist. Jeder Zwilling sieht den anderen langsamer altern als sich selbst.
b) Verwenden Sie Raumzeit-Diagramme, um zu zeigen, wie der abrupte Wechsel des Reisenden von einem Bezugssystem zum anderem seine Definition der Gleichzeitigkeit verändert. Im neuen Bezugssystem des Reisenden ist sein Zwilling plötzlich viel älter, als er es im ursprünglichen System des Reisenden war.
Lösung:
a) Sehen wir uns Arts Reise an, solange er nicht umkehrt:
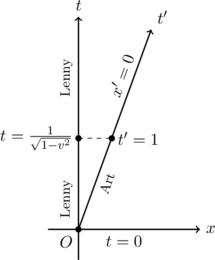
Dem Punkt ![]() entspricht ein Zeitpunkt in Arts Ruhesystem
entspricht ein Zeitpunkt in Arts Ruhesystem ![]() . Für den Punkt
. Für den Punkt ![]() ergibt sich der entsprechende Zeitpunkt
ergibt sich der entsprechende Zeitpunkt ![]() für Lenny:
für Lenny:
![]()
Für Lenny ist
Aber diese Sicht ist völlig symmetrisch! Betrachten wir die Situation einmal mit Art als ruhendem Beobachter, der Lenny auf dem Planeten Erde in umgekehrter Richtung davonfliegen sieht:
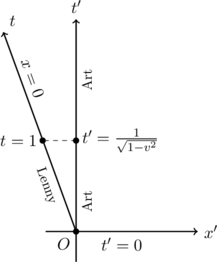
Die Lorentz-Transformation ist nun für den Punkt
![]()
Mit derselben Lorentz-Transformation und vertauschtem
Aufgabe 3.1
Beweisen Sie mit Hilfe der Definition von ![]() die Gl. 3.7.
die Gl. 3.7.
Lösung:
Für Gl. 3.7 gilt nach Definition der ![]() :
:
![]()
Aufgabe 5.1
Zeigen Sie, dass ![]() dieselbe Bedeutung hat wie
dieselbe Bedeutung hat wie ![]() .
.
Lösung:
![]() und
und ![]() sind hier einfach nur Summenindizes; das Summenzeichen ist ja durch die Summenkonvention ausgeblendet:
sind hier einfach nur Summenindizes; das Summenzeichen ist ja durch die Summenkonvention ausgeblendet:
![Rendered by QuickLaTeX.com \[ A^\nu A_\nu = \sum_{\nu=0}^{3} A^\nu A_\nu = \sum_{\mu=0}^{3} A^\mu A_\mu = A^\mu A_\mu. \]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-e26d8652ce1364147fb5c5e212e8fc71_l3.png)
Aufgabe 5.2
Schreiben Sie einen Ausdruck, der die Wirkung von Gl. 5.20 rückgängig macht. Anders ausgedrückt: Wie geht es „zurück“?
Lösung:
Gl. 5.20 beschreibt die Transformation ![]() , also das Senken eines Index. Dabei ist
, also das Senken eines Index. Dabei ist ![]() der metrische Tensor mit
der metrische Tensor mit ![]() und 0 sonst.
und 0 sonst.
Die Umkehrung, also das Heben des Index geschieht einfach durch ![]() .
.
Da in der Speziellen Relativitätstheorie ![]() gilt, wird also jeweils nur die 0. Komponente von
gilt, wird also jeweils nur die 0. Komponente von ![]() mit
mit ![]() multipliziert; die anderen Komponenten bleiben unverändert. In der ART ist der metrische Tensor komplizierter.
multipliziert; die anderen Komponenten bleiben unverändert. In der ART ist der metrische Tensor komplizierter.
Aufgabe 6.1
Gegeben sei die Transformationsgleichung (Gl. 6.3) für die kontravarianten Komponenten eines Vierervektors ![]() , wobei
, wobei ![]() eine Lorentz-Transformations-Matrix ist. Zeigen Sie, dass die Lorentz-Transformation für die kovarianten Komponenten von
eine Lorentz-Transformations-Matrix ist. Zeigen Sie, dass die Lorentz-Transformation für die kovarianten Komponenten von ![]()
![]()
lautet, wobei gilt
![]()
Lösung:
Die Transformationsgleichung 6.3 lautet
![]()
Zum Heben und Senken eines Index benutzen wir den metrischen Tensor (s. auch Aufgabe 5.2.). Es gilt
![]()
wobei
Aufgabe 6.2
Ausdruck Gl. 6.28 wurde durch Identifizieren des Index ![]() mit der
mit der ![]() -Komponente des Raums hergeleitet, und nach Summation über
-Komponente des Raums hergeleitet, und nach Summation über ![]() für die Werte (1, 2, 3). Warum enthält Ausdruck Gl. 6.28 keinen Term mit
für die Werte (1, 2, 3). Warum enthält Ausdruck Gl. 6.28 keinen Term mit ![]() ?
?
Lösung:
Wir haben Gl. 6.28
![]()
![]()
![]()
Aufgabe 8.1
Betrachten Sie eine ruhende elektrische Ladung, ohne Anwesenheit weiterer elektrischer oder magnetischer Felder. Wie lautet in Ausdrücken von ![]() die
die ![]() -Komponente des elektrischen Feldes eines Beobachters, der sich mit Geschwindigkeit
-Komponente des elektrischen Feldes eines Beobachters, der sich mit Geschwindigkeit ![]() in negativer
in negativer ![]() -Richtung bewegt? Wie lauten die
-Richtung bewegt? Wie lauten die ![]() – und
– und ![]() -Komponenten? Was sind die dazugehörenden Komponenten des magnetischen Feldes?
-Komponenten? Was sind die dazugehörenden Komponenten des magnetischen Feldes?
Lösung:
Der elektromagnetische Feldtensor hat die Gestalt
![Rendered by QuickLaTeX.com \[F_{\mu \nu} = \begin{pmatrix}0 & -E_x & -E_y & -E_z \\+E_x & 0 & 0 & 0 \\+E_y & 0 & 0 & 0 \\+E_z & 0 & 0 & 0\end{pmatrix},\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-9689d5f69eef007ab128e13020b514c0_l3.png)
da kein Magnetfeld existiert. Der Feldtensor für das sich nach links bewegende Teilchen mit Geschwindigkeit
![]()
wie in Abschnitt 8.1.1 beschrieben.
Aufgabe 8.2
Art sitzt im Bahnhof, als der Zug vorbeifährt. Wie lautet in Termen von Lennys Feldkomponenten die ![]() -Komponente von
-Komponente von ![]() , die von Art beobachtet wird? Wie lauten die
, die von Art beobachtet wird? Wie lauten die ![]() – und
– und ![]() -Komponenten? Was sind die dazugehörenden Komponenten des magnetischen Feldes, das Art wahrnimmt?
-Komponenten? Was sind die dazugehörenden Komponenten des magnetischen Feldes, das Art wahrnimmt?
Lösung:
Aufgabe 8.3
Berechnen Sie in Einsteins Beispiel alle Komponenten der elektrischen und magnetischen Felder im Ruhesystem des Elektrons.
Lösung:
Aufgabe 8.4
Benutzen Sie die zweite Gruppe der Maxwell-Gleichungen aus Tab. 8.1 zusammen mit den Vektoridentitäten aus Abschnitt 8.2.1, um die Kontinuitätsgleichung herzuleiten.
Lösung:
Aufgabe 11.1
Zeigen Sie, dass ![]() der Poynting-Vektor ist.
der Poynting-Vektor ist.
Lösung:
Aufgabe 11.2
Berechnen Sie ![]() und
und ![]() in Termen der Feldkomponenten
in Termen der Feldkomponenten ![]() und
und ![]() .
.
Lösung:
Aufgabe A.1
Leiten Sie Gleichung A.13 aus Gleichung 9.18 her.
Hinweis: Die Ableitung folgt derselben Logik wie die Ableitung von Gleichung 9.22 in Abschnitt 9.2.5.


Sehr geehrter Herr Sippel,
in der Lösung zur Aufgabe 1.2 müßte es meiner Meinung nach heißen :
Für Lenny ist t > 1, …
Für Lenny ist t = \frac{1}{\sqrt{1-v^2}} > 1, also altert Lenny aus Arts Sicht SCHNELLER , denn es ist MEHR Zeit vergangen.
Aber diese Sicht ist völlig symmetrisch! Betrachten wir die Situation einmal mit Art als ruhendem Beobachter, der Lenny auf dem Planeten Erde in umgekehrter Richtung davonfliegen sieht:
Rendered by QuickLaTeX.com
Die Lorentz-Transformation ist nun für den Punkt t=1 in Lenny Ruhesystem x=0:
\[ t‘ = \frac{t-vx}{\sqrt{1-v^2}} = \frac{1}{\sqrt{1-v^2}}.\]
t` > 1
Mit derselben Lorentz-Transformation und vertauschtem t und t‘ sieht der auf der Erde davonfliegende Lenny den in der Rakete zurückbleibenden Art SCHNELLER altern. Dies ist das Wesen der SRT: Keines der beiden Bezugssysteme ist bevorzugt. Nur was geschieht am Umkehrpunkt?
Ich hoffe, ich habe mich nicht geirrt. Über eine kurze Antwort würde ich mich freuen.
Mein Physikstudium liegt über 60 Jahre zurück.
Ich habe mir vorgenommen, Das theoretische Minimum Bd I bis III zu lesen. Mal sehen , wie weit ich komme. Ich habe wohl mit BdIII begonnen, werde mich jetzt aber erst mal mit BdI beschäftigen.
Mit freundliche Grüßen
Michael Spiess
Hallo,
richtig, ich habe Art und Lenny vertauscht. Jeder sieht die Uhr des wegfliegenden Freundes (egal ob in der Rakete oder auf der Erde sitzend) langsamer ticken (d.h. t > t‘) und somit seinen Freund schneller altern. Habe ich korrigiert.
Das „Paradoxon“ kommt erst dadurch zustande, dass Arts Rakete umkehrt und nun den von Lenny bereits ausgesandten Lichtwellen entgegenreist und diese sehr schnell aufsammelt (Zeitraffer). Dies sollte ich in 1.2 b zeigen, aber ich habe noch kein schönes Bild dafür.
Vielen Dank für den Hinweis, und viel Spaß beim Lesen!
Hallo,
wenn die Rakete am Zielort anhält (bremst -> deshalb kein IS -> deshalb invariant), dann fallen beide Koordinatensysteme wieder aufeinander (x=0, x’=0, t=0, t’=0). Deshalb reicht es doch aus, das GLEICHE RZ-Diagramm so nach links zu drehen (Rotation), dass die Reiseroute mit der Rückreise identisch ist. Aber auch hier ergibt sich wieder das gleiche Ergebnis für t‘.
Mit dem ‚Zeitraffer bzw. Aufsammeln‘ hat das nichts zu tun… Das Paradoxon entsteht, weil es in einem Fall KEIN Inertialsystem ist (beschleunigen, bremsen, im Stand umkehren, beschleunigen, bremsen). Meine Meinung…. siehe Videos.
(Bild als png vorhanden).
Mfg,
HP Kiermaier
Hallo,
wir müssen da wohl zwei Dinge unterscheiden, einmal die Darstellung im („abstrakten“) Raumzeit-Diagramm, und andererseits das Erlebte in „unserer“ Welt. Und da sieht der Reisende tatsächlich das gesamte Geschehen (im Zeitraffer), da ja keine Information verlorengehen kann. Oder?
Schöne Grüße
Heiko