Aufgabe 11.1:
Beweisen Sie Gl. 11.3. Beweisen Sie weiterhin, dass
![]()
gilt.
Gl. 11.3 lautet:
![]()
Lösung:
Wir zeigen die Gleichung Gl. 11.3 durch einfaches Ausrechnen für ![]() . Die Komponenten des Kreuzprodukts lauten:
. Die Komponenten des Kreuzprodukts lauten:
![Rendered by QuickLaTeX.com \[\begin{split}(\vec{V} \times \vec{A})_1 &= V_2A_3 - V_3A_2 \\(\vec{V} \times \vec{A})_2 &= V_3A_1 - V_1A_3 \\(\vec{V} \times \vec{A})_3 &= V_1A_2 - V_2A_1.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-6327dcb90d69a05137c442d23fccc0c3_l3.png)
Die rechte Seite lautet für ![]() :
:
![]()
Die Doppelsumme ergibt nur noch zwei einzelne Summanden, da ![]() ist, wenn
ist, wenn ![]() oder
oder ![]() ist. Entsprechend folgt für
ist. Entsprechend folgt für ![]() und
und ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split}\sum_j \sum_k \epsilon_{2jk} V_j A_k &=\epsilon_{231} V_3 A_1 + \epsilon_{213} V_1 A_3 = +V_3 A_1 - V_1 A_3\\\sum_j \sum_k \epsilon_{3jk} V_j A_k &=\epsilon_{312} V_1 A_2 + \epsilon_{321} V_2 A_1 = +V_1 A_2 - V_2 A_1.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-19748557f09025238fd07b43aac2c277_l3.png)
Auch der Beweis für
![]()
Wir bemerken zunächst, dass beide Seiten der Gleichung zu 0 werden, wenn ![]() ist. Links steht zweimal dasselbe mit verschiedenen Vorzeichen, und rechts wird
ist. Links steht zweimal dasselbe mit verschiedenen Vorzeichen, und rechts wird ![]() .
.
Weiterhin besteht die linke Summe nur aus einem einzelnen Summanden, da bei vorgegeben ![]() und
und ![]()
![]() ist für
ist für ![]() oder
oder ![]() .
.
Unter diesen Voraussetzungen braucht man also nur die Fälle ![]() zu untersuchen, mit entsprechenden
zu untersuchen, mit entsprechenden ![]() . Dies sind aber genau die Gleichungen aus 11.3. Zum Beispiel gilt
. Dies sind aber genau die Gleichungen aus 11.3. Zum Beispiel gilt
![Rendered by QuickLaTeX.com \[\begin{split}V_1A_2 - V_2A_1 &= \sum_k \epsilon_{12k} (V \times A)_k = \epsilon_{123} (V \times A)_3 = +(V \times A)_3\\V_2A_1 - V_1A_2 &= \sum_k \epsilon_{21k} (V \times A)_k = \epsilon_{213} (V \times A)_3 = -(V \times A)_3.\\\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-f32af28b9d37ef40d5fc478032edb342_l3.png)
Aufgabe 11.2:
Beweisen Sie Gl. 11.4.
![]()
Lösung:
Gl. 11.4 besagt, dass die Rotation eines Gradienten verschwindet. Der Gradient von V ist ein Vektor mit den drei Komponenten
![Rendered by QuickLaTeX.com \[\begin{split}(\vnabla V)_x &= \pd{V}{x}\\(\vnabla V)_y &= \pd{V}{y}\\(\vnabla V)_z &= \pd{V}{z}.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-d092ef2bf7933f5cfecb0a810b71d162_l3.png)
Die Rotation dieses Gradienten ist ein weiterer Vektor mit den Komponenten
![Rendered by QuickLaTeX.com \[\begin{split}(\vnabla \times \vnabla V)_x &= \pd{}{y} \pd{V}{z} - \pd{}{z} \pd{V}{y} = \frac{\partial^2 V}{\partial y \partial z} - \frac{\partial^2 V}{\partial z \partial y} = 0\\(\vnabla \times \vnabla V)_y &= \pd{}{z} \pd{V}{x} - \pd{}{x} \pd{V}{z} = \frac{\partial^2 V}{\partial z \partial x} - \frac{\partial^2 V}{\partial x \partial z} = 0\\(\vnabla \times \vnabla V)_z &= \pd{}{x} \pd{V}{y} - \pd{}{y} \pd{V}{x} = \frac{\partial^2 V}{\partial x \partial y} - \frac{\partial^2 V}{\partial y \partial x} = 0.\\\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-e57cdce006427bdd95530c3e3ad97a68_l3.png)
Die Komponenten sind alle 0, da die Reihenfolge der Differentiation bei den zweiten Ableitungen beliebig ist.
Aufgabe 11.3:
Zeigen Sie, dass die Vektorpotentiale in Gleichungen Gl. 11.8 und Gl. 11.9 dasselbe homogene Magnetfeld erzeugen. Das bedeutet, dass sie sich nur um einen Gradienten unterscheiden. Finden Sie den Skalar, dessen Gradient zu 11.8 addiert, die Gleichungen Gl. 11.9 ergeben.
Lösung:
Gl. 11.8
![Rendered by QuickLaTeX.com \[\begin{split}A_x &= 0 \\A_y &= b x \\A_z &= 0.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-64185ed6da62b4fbf37db19172cc5b5d_l3.png)
Gl. 11.9
![Rendered by QuickLaTeX.com \[\begin{split}A'_x &= -b y \\A'_y &= 0 \\A'_z &= 0.\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-b5ad58fc6c8108cfde474e49c02b42f4_l3.png)
Die beiden Vektorpotentiale lauten
![Rendered by QuickLaTeX.com \[A=\begin{pmatrix}0\\bx\\0\end{pmatrix},A'=\begin{pmatrix}-by\\0\\0\end{pmatrix}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-df7b8181f45df9f813ace923f09d9443_l3.png)
Gesucht ist ein Skalar, dessen Gradient zu
![]()
![Rendered by QuickLaTeX.com \[ \vnabla V= A'-A =\begin{pmatrix}-by\\-bx\\0\end{pmatrix}. \]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-21074dd6031583e035959e4c53e9cf5d_l3.png)
Somit ist
![]()
Aufgabe 11.4:
Stellen Sie mit Hilfe der Hamilton-Funktion aus Gl. 11.24 die Hamiltonschen Bewegungsgleichungen auf und zeigen Sie, dass man daraus die Newton-Lorentz-Gleichungen erhält.
Lösung:
Die Newton-Lorentz-Gleichung lautet
![]()
Gleichung 11.24 lautet:
![]()
Dabei steht der Index ![]() für die Koordinaten
für die Koordinaten ![]() . Die Hamilton-Gleichungen für
. Die Hamilton-Gleichungen für ![]() und
und ![]() lauten daher:
lauten daher:
![Rendered by QuickLaTeX.com \begin{align*} \dot{q}_x &= \pd{\Ham}{p_x} = \frac{2}{2m} \left[ p_x - \frac{e}{c} A_x\right] \Rightarrow m\dot{q}_x = p_x - \frac{e}{c} A_x\\ \dot{q}_y &= \pd{\Ham}{p_y} = \frac{2}{2m} \left[ p_y - \frac{e}{c} A_y\right] \Rightarrow m\dot{q}_y = p_y - \frac{e}{c} A_y\\\dot{q}_z &= \pd{\Ham}{p_z} = \frac{2}{2m} \left[ p_z - \frac{e}{c} A_z\right] \Rightarrow m\dot{q}_z = p_z - \frac{e}{c} A_z. \end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-e2d5f6e1fdbfd78f9aaf28599589f9d1_l3.png)
Die Hamilton-Gleichung für ![]() ist etwas komplizierter, da
ist etwas komplizierter, da ![]() eine Funktion von
eine Funktion von ![]() ist:
ist:
![Rendered by QuickLaTeX.com \begin{align*}\dot{p}_x &= -\pd{\Ham}{q_i}\\&= \frac{2}{2m} \big[ p_x - \frac{e}{c} A_x\big]\frac{e}{c}\pd{A_x}{x} + \frac{2}{2m} \left[ p_x - \frac{e}{c} A_y\right]\frac{e}{c}\pd{A_y}{x} + \frac{2}{2m} \left[ p_x - \frac{e}{c} A_z\right]\frac{e}{c}\pd{A_z}{x}\\&= \frac{1}{m}\frac{e}{c} \big[ (p_x - \frac{e}{c} A_x) \pd{A_x}{x} + (p_y - \frac{e}{c} A_y) \pd{A_y}{x} + (p_z - \frac{e}{c} A_z) \pd{A_z}{x} \big]\\&= \frac{1}{m}\frac{e}{c} \big[ m\dot{x} \pd{A_x}{x} + m\dot{y} A_y) \pd{A_y}{x} + m\dot{z} \pd{A_z}{x} \big]\\&= \frac{e}{c} \big[ \dot{x} \pd{A_x}{x} + \dot{y} \pd{A_y}{x} + \dot{z} \pd{A_z}{x} \big].\end{align*}](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-726409b645ca9ec3052daf06e1ff1a9e_l3.png)
Die Gleichungen für ![]() und
und ![]() sehen entsprechend aus.
sehen entsprechend aus.
Für die Newton-Lorentz-Gleichung brauchen wir die zweite Zeitableitung von ![]() :
:
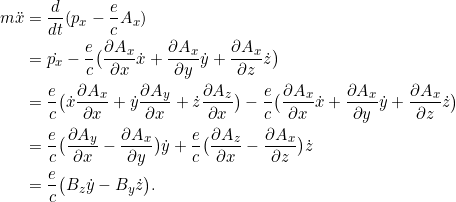
Das ist die ![]() -Komponente der Newton-Lorentz-Gleichung
-Komponente der Newton-Lorentz-Gleichung ![]() . Die beiden anderen Komponenten folgen ganz genauso.
. Die beiden anderen Komponenten folgen ganz genauso.
Aufgabe 11.5:
Zeigen Sie, dass die Lösungen der Gleichungen Gl. 11.25 und Gl. 11.26 Kreisbahnen in der ![]() -Ebene sind. Drücken Sie den Radius der Bahnen in Größen der Geschwindigkeit aus.
-Ebene sind. Drücken Sie den Radius der Bahnen in Größen der Geschwindigkeit aus.
![Rendered by QuickLaTeX.com \[\begin{split}a_y &= - \dfrac{e b}{m c} v_x \;\;\;\;\; (11.25) \\a_x &= +\dfrac{e b}{m c} v_y \;\;\;\;\;\;(11.26)\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-28243b90c540af798a3f70fe82411eec_l3.png)
Lösung:
Die Gleichungen 11.25 und 11.26 lauten
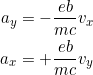
Mit dem Ansatz
![]()
der eine Kreisbewegung mit Radius
![]()
und damit
![]()
Setzen wir
Für den Betrag der Geschwindigkeit gilt:
![]()
so dass der Radius
![]()
