Lösungen Band IV, Vorlesung 3

Aufgabe 3.1

Erklären Sie, warum ein Raum flach sein kann, und trotzdem die Christoffelsymbole nicht null sein müssen.

Lösung:

Aufgabe 3.2

Erklären Sie, warum die kovariante Ableitung des metrischen Tensors immer null ist.

Lösung:

Aufgabe 3.3:

Bestimmen Sie auf der Erde mit den Polarkoordinaten $\theta$ für die Breite und $\phi$ für die Länge

den metrischen Tensor $g_{mn}$
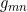
seine Inverse $g^{mn}$
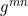
die Christoffelsymbole im Punkt $(\theta,\phi)$

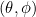
Lösung:

Wir verwenden die sphärischen Polarkoordinaten, also Längen- und Breitengrade.

Rendered by QuickLaTeX.com

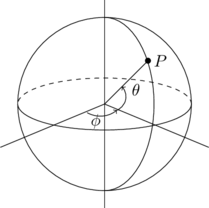
1: Die Metrik: Wir müssen zuerst einmal das Quadrat der Länge des Linienelements $ds^2 = dx^2 + dy^2 +dz^2$ in den gewohnten Kugelkoordinaten in eine Form mit $d\theta^2$ und $d\phi^2$ überführen. Dazu leiten wir aus den Kugelkoordinaten

$\begin{equation*}\begin {split}x &= r \sin \theta \cos \phi\\y &= r \sin \theta \sin \phi\\z &= r \cos \theta, \end{split}\end{equation*}$

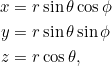
wobei auf der Einheitssphäre $r=1$ gilt, die Werte von $dx^2,dy^2,dz^2$ ausgedrückt in $d\theta^2$ und $d\phi^2$ her:

$\begin{equation*}\begin {split}dx &= \cos \theta \cos \phi d\theta - \sin \theta \sin \phi d\phi\\dx^2 &= \cos^2 \theta \cos^2 \phi d\theta^2 - 2 \cos \theta \cos \phi \sin \theta \sin \phi\, d\theta \,d\phi + \sin^2 \theta \sin^2 \phi\, d\phi^2,\\dy &= \cos \theta \sin \phi d\theta - \sin \theta \cos \phi d\phi\\dy^2 &= \cos^2 \theta \sin^2 \phi d\theta^2 + 2 \cos \theta \sin \phi \sin \theta \cos \phi \, d\theta \,d\phi + \sin^2 \theta \cos^2 \phi\, d\phi^2\\dz &= - \sin \theta d\theta\\ dz^2 &= - \sin^2 \theta d\theta^2\end{split}\end{equation*}$

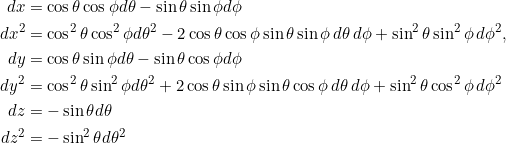
Bei der Summe heben sich die gemischten Terme bei $dx^2$ und $dy^2$ glücklicherweise auf (was an der Orthogonalität der Kugelkoordinaten liegt), und es bleibt übrig, wenn wir nach $d\theta^2$ und $d\phi^2$ sortieren:

$\begin{equation*}\begin {split}ds^2 &= dx^2 + dy^2 +dz^2\\&= d\theta^2(\cos^2\theta \cos^2 \phi + \cos^2\theta \sin^2 \phi + \sin^2 \theta ) + d\phi^2(\sin^2 \theta \cos^2 \phi + \sin^2 \theta \sin^2 \phi )\\&= d\theta(\cos^2 \theta + \sin^2 \theta) + d\phi^2 (\cos^2\theta)\\&= d\theta^2 + \cos^2\theta\,d\phi^2.\end{split}\end{equation*}$

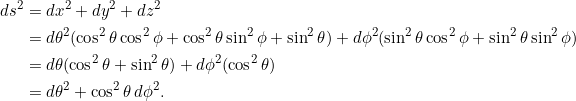
In Matrixschreibweise für die Metrik erhalten wir damit für $X^1=\theta$ und $X^2=\phi$ :

$g_{mn}= \begin{pmatrix} 1&0\\0& \cos^2 \theta \end{pmatrix}.$

Das ist plausibel. Die Koordinatenlinien, d.h. Längen- und Breitengrade stehen senkrecht aufeinander, damit wird $g$ durch eine Diagonalmatrix dargestellt. Die Differentiale der Breitengrade $d\phi$ sind überall gleich groß, während die Differentiale der Längengrade $d\theta$ vom Äquator aus zu den Polen immer kleiner werden.

2. Die inverse Metrik: Dies ist recht einfach wegen der Diagonalform der Metrik, es ist

$g^{mn} = \begin{pmatrix} 1&0\\0& \cos^{-2} \theta \end{pmatrix}$

3. Die Christoffelsymbole: Auf der zweidimensionalen Fläche müssen wir acht Christoffelsysmbole $\Gamma^t_{mn}$ berechnen, wobei je zwei Paare wegen der Symmetrie in $m$ und $n$ gleich sind. Sechs bleiben übrig; immer noch eine ganze Menge. Die Metrik ist aber recht einfach, fast schon die Einheitsmatrix. Sehen wir uns die Formel für die Christoffelsymbole einmal an:

(1) $\begin{equation*} \Gamma^t_{mn} = \frac{1}{2} g^{rt} [\partial_n g_{rm} + \partial_m g_{rn} -\partial_r g_{mn}]\end{equation*}$

Wir brauchen also zunächst einmal die Inverse der Metrik; dass ist leicht, es ist offensichtlich

$g^{mn} = \begin{pmatrix} 1&0\\0& \cos^{-2} \theta \end{pmatrix}$

Dann stehen in den eckigen Klammern verschiedene partielle Ableitungen von $g_{mn}$ . Diese sind aber fast alle null, die einzige partielle Ableitung ungleich null ist

$\partial_1g_{22} = \partial_\theta \cos^2\theta = - 2 \cos \theta \sin \theta$

Damit die Summe in Gleichung (1) ungleich null ist, muss also gelten: $t=r$ , und es muss in den eckigen Klammer ein $\partial_1g_{22}$ vorkommen. Probieren wir es:

$t=1 \rightarrow \Gamma^1_{mn} = \frac{1}{2} g^{11} [\partial_n g_{1m} + \partial_m g_{1n} -\partial_1 g_{mn}]$

In den eckigen Klammern kann nur der dritte Term ungleich null sein, und dies auch nur für $m = n = 2$ . Es ist dann

$\Gamma^1_{22} = \frac{1}{2} g^{11} [\partial_2 g_{12} + \partial_2 g_{12} -\partial_1 g_{22}] = \frac{1}{2} 1 [0 + 0 + 2 \cos \theta \sin \theta ] = \cos\theta \sin \theta.$

Weiter ist $\Gamma^1_{11} = \Gamma^1_{12} = \Gamma^1_{21} = 0$ .

Und weiter ist

$t=2 \rightarrow \Gamma^2_{mn} = \frac{1}{2} g^{22} [\partial_n g_{2m} + \partial_m g_{2n} -\partial_2 g_{mn}]$

Hier können umgekehrt nur die beiden ersten Terme in der Summe ungleich null sein, und zwar nur für $m=1, n=2$ bzw. $m=2, n=1$ . Wir rechnen den ersten Fall aus, der zweite ergibt ja, wie wir wissen, denselben Wert:

$t=2 \rightarrow \Gamma^2_{12} = \frac{1}{2} g^{22} [\partial_2 g_{21} + \partial_1 g_{22} -\partial_2 g_{12}] = \frac{1}{2} \frac{1}{\cos^2\theta} [ -2 \cos \theta \sin \theta ] = - \frac{\sin \theta}{\cos \theta} = - \tan \theta.$

Dies ist auch der Wert für $\Gamma^2_{21}$ , während $\Gamma^2_{11} = \Gamma^2_{22} = 0$ ist.

Durch die einfache Form der Metrik konnten wir uns mit ein paar kombinatorischen Argumenten behelfen. Bei weniger symmetrischen Fällen und in höheren Dimensionen wird es natürlich ungeheuer kompliziert, und hier helfen uns dann Computer-Algebra-Systeme wie Mathematica, oder Programmiersprachen wie Python, die über entsprechende Bibliotheken verfügen.