Aufgabe 3.1
Beweisen Sie: Ist ein Vektorraum ![]() -dimensional, so kann man eine Orthonormalbasis aus
-dimensional, so kann man eine Orthonormalbasis aus ![]() Vektoren finden, gebildet aus den Eigenvektoren eines hermiteschen Operators.
Vektoren finden, gebildet aus den Eigenvektoren eines hermiteschen Operators.
Lösung:
Dieser Satz ist ein wichtiges Ergebnis aus der Linearen Algebra, einer mathematischen Disziplin, die sich mit linearen Vektorräumen befasst. Da unsere Zustandsräume lineare Vektorräume sind, lassen sich alle Ergebnisse der Linearen Algebra anwenden. Aber wir haben den Satz praktisch im Abschnitt 3.1.5 (S. 41f) bewiesen. Man kann aus den Eigenvektoren eines hermiteschen Operators eine Orthonormalbasis auswählen. Ist der Zustandsraum N-dimensional, so gibt es N Eigenwerte. Die Eigenvektoren zweier verschiedener Eigenwerte sind jeweils orthogonal. Sind nun alle Eigenwerte verschieden, so können wir zu jedem Eigenwert einen Eigenvektor auswählen und diesen normieren. Dadurch haben wir unsere Orthonormalbasis. Aber auch bei Entartung eines Eigenwerts, d.h. wenn zwei oder mehr Eigenwerte übereinstimmen (d.h. wenn ein Eigenwert ein sogenannter mehrfacher Eigenwert ist), können wir mehrere (der Vielfachheit entsprechende) Eigenvektoren dazu finden, die paarweise orthogonal sind. Eine zentrale Rolle bei dieser Aussage spielt das in 3.1.6 beschrieben Gram-Schmidtsche Orthonormalisierungsverfahren.
Aufgabe 3.2
Zeigen Sie, dass Gl. 3.16 die eindeutige Lösung zu Gleichungen 3.14 und 3.15 ist.
Lösung:
Wir suchen einen hermiteschen Operator ![]() , der die beiden Gleichungen
, der die beiden Gleichungen
![]()
erfüllt. Da
![]()
wobei
Dadurch werden die beiden Gleichungen zu
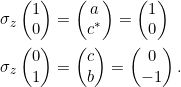
Man liest sofort ab:
![]()
Aufgabe 3.3
Berechnen Sie die Eigenvektoren und Eigenwerte von ![]() .
.
Hinweis: Nehmen Sie an, dass der Eigenvektor ![]() die Form
die Form
![]()
Lösung:
Wir verwenden den empfohlenen Ansatz und erhalten:
![]()
Die letzte Gleichheit folgt aus den Additionstheoremen der Trigonometrie. Für die beiden möglichen Eigenwerte ![]() und
und ![]() muss nun gelten:
muss nun gelten:
![]()
Wir erhalten eine einfache Lösung für
![]()
Also ist
![]()
Von dieser Lösung ausgehend können wir eine zweite Lösung finden wegen den Identitäten ![]() . Setzen wir
. Setzen wir ![]() , so gilt
, so gilt
![]()
Wir haben also einen Eigenvektor zum Eigenwert ![]() gefunden, wenn wir
gefunden, wenn wir ![]() setzen.
setzen.
Das sah nun ziemlich nach Raten aus. Wir hatten ja eine vorgegebene Form des Eigenvektors, und durch Ausprobieren dann die beiden Eigenwerte samt Eigenvektoren gefunden. Gibt es denn auch ein allgemeines Rezept, wenn man die Form des Eigenvektors nicht ahnt? Tatsächlich gibt es ein Verfahren, die Eigenwerte zu bestimmen. Dies geschieht mit Hilfe des charakteristischen Polynoms einer Matrix, und im Internet findet man dazu zahlreiche Erklärungen.
Aufgabe 3.4
Seien ![]() ,
, ![]() und
und ![]() . Die Winkel
. Die Winkel ![]() und
und ![]() sind nach den üblichen Konventionen der sphärischen Koordinaten definiert (Abb. 3.2). Berechnen Sie die Eigenwerte und Eigenvektoren für die Matrix in Gl. 3.23.
sind nach den üblichen Konventionen der sphärischen Koordinaten definiert (Abb. 3.2). Berechnen Sie die Eigenwerte und Eigenvektoren für die Matrix in Gl. 3.23.
Lösung:
Nach Gl. 3.23 ist
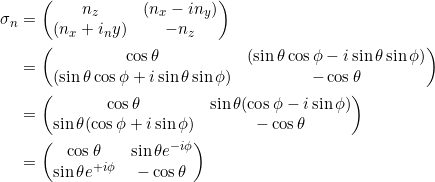
Das charakteristische Polynom lautet
![]()
Es hat die beiden Nullstellen
Wir müssen nun die Eigenvektoren bestimmen.
Wir beginnen mit ![]() . Versuchen wir es mit dem Ansatz aus Aufgabe 3.3:
. Versuchen wir es mit dem Ansatz aus Aufgabe 3.3:
![]()
Dieser Ausdruck lässt sich wegen der Terme
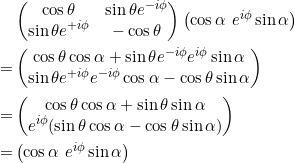
Wir erhalten also folgende Gleichungen zum Eigenwert ![]()
![]()
und damit
![]()
Für eine Ansatz für Eigenwert ![]() benutzen wir die Tatsache, dass
benutzen wir die Tatsache, dass ![]() gilt, denn die Eigenvektoren stehen senkrecht aufeinander. Damit erraten wir
gilt, denn die Eigenvektoren stehen senkrecht aufeinander. Damit erraten wir
![]()
Wir können dies noch überprüfen:

Aufgabe 3.5
Nehmen Sie an, ein Spin ist so präpariert, dass ![]() ist. Die Apparatur wird dann in
ist. Die Apparatur wird dann in ![]() -Richtung gedreht und
-Richtung gedreht und ![]() gemessen. Wie groß ist die Wahrscheinlichkeit, dass das Ergebnis +1 ist? Beachten Sie, dass
gemessen. Wie groß ist die Wahrscheinlichkeit, dass das Ergebnis +1 ist? Beachten Sie, dass ![]() ist, mit derselben Konvention für
ist, mit derselben Konvention für ![]() .
.
Lösung:
Wir können es uns etwas einfacher machen, indem wir unser Koordinatensystem so drehen, dass ![]() mit der
mit der ![]() -Achse zusammenfällt. In diesem Fall ist
-Achse zusammenfällt. In diesem Fall ist ![]() , und der Spin „zeigt nach oben“, d.h. der Zustand ist
, und der Spin „zeigt nach oben“, d.h. der Zustand ist ![]() .
.
Wir drehen die Apparatur nun so , dass sie in Richtung von ![]() zeigt. Dann ist
zeigt. Dann ist ![]() wie in Aufgabe 3.4 beschrieben, also
wie in Aufgabe 3.4 beschrieben, also![]() ,
, ![]() und
und ![]() , wobei
, wobei ![]() der Winkel mit der
der Winkel mit der ![]() -Achse und damit zu
-Achse und damit zu ![]() ist. Wieder ist
ist. Wieder ist
![]()
Die Eigenwerte lauten ![]() und
und ![]() mit den Eigenvektoren
mit den Eigenvektoren
![]()
Damit gilt:
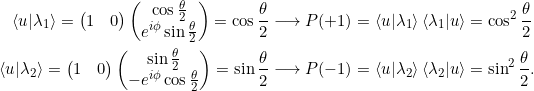
Es ist ![]() .
.

Ich glaube in Aufgabe 3.4 gibt es ein Problem mit der Vektor/Matrix-Darstellung. Dadurch fehlt leider komplett die Nachvollziehbarkeit. Trotzdem vielen Dank für die Unterstützung mit dieser Seite!
Stimmt, die Formatierung war völlig kaputt. Ich musst etwas basteln, um das wieder hinzukriegen, vielen Dank für den Hinweis!