Aufgabe 2.1
Beweisen Sie, dass der Vektor ![]() in Gl. 2.5 orthogonal auf dem Vektor
in Gl. 2.5 orthogonal auf dem Vektor ![]() in Gl. 2.6 steht.
in Gl. 2.6 steht.
Lösung:
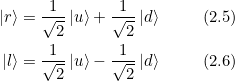
Es ist damit
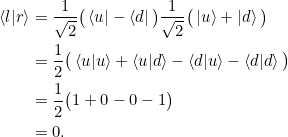
Aufgabe 2.2
Beweisen Sie, dass ![]() und
und ![]() alle Bedingungen aus den Gleichungen 2.7, 2.8 und 2.9 erfüllen. Sind sie dadurch eindeutig bestimmt?
alle Bedingungen aus den Gleichungen 2.7, 2.8 und 2.9 erfüllen. Sind sie dadurch eindeutig bestimmt?
Lösung:
Das ist nun einmal wirklich reine Fleißarbeit. Es sind
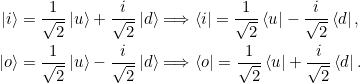
Gleichungen 2.7 (Orthogonalität)
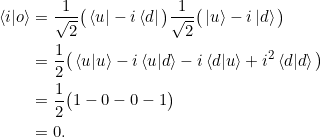
Gleichungen 2.8
Wir berechnen die Produkte mit ![]() und
und ![]() :
:
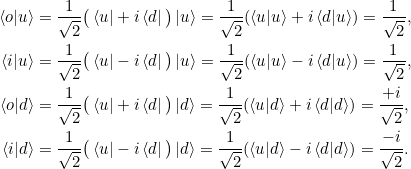
Wenn wir nun die Antisymmetrie verwenden, so sehen wir die Gleichungen aus 2.8:
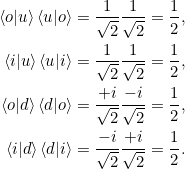
Gleichungen 2.9
Es sind ![]() und
und ![]() . Mittlerweile sehen wir, wie das läuft: Die gemischten Terme fallen weg wegen
. Mittlerweile sehen wir, wie das läuft: Die gemischten Terme fallen weg wegen ![]() , und übrig bleiben die Terme
, und übrig bleiben die Terme ![]() :
:
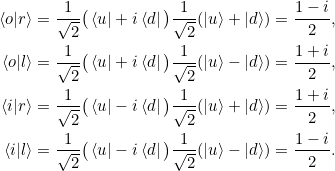
und damit wegen der Antisymmetrie ![]() und
und ![]() :
:
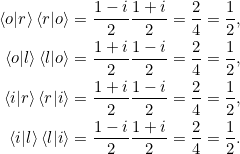
Auf die Frage nach der eindeutigen Bestimmtheit gehen wir in Aufgabe 2.3 ein.
Aufgabe 2.3
Vergessen wir einmal, dass uns die Gleichungen 2.10 funktionierende Definitionen für ![]() und
und ![]() ausgedrückt in Termen von
ausgedrückt in Termen von ![]() und
und ![]() geben, und nehmen wir an, die Komponenten
geben, und nehmen wir an, die Komponenten ![]() ,
, ![]() ,
, ![]() und
und ![]() seien noch unbekannt:
seien noch unbekannt:
![]()
a) Zeigen Sie mit Hilfe der Gleichungen 2.8, dass gilt
![]()
b) Zeigen Sie mit dem ersten Resultat und den Gleichungen 2.9, dass gilt
![]()
c) Zeigen Sie, dass ![]() und
und ![]() rein imaginär sein müssen.
rein imaginär sein müssen.
Ist ![]() rein imaginär, so können
rein imaginär, so können ![]() und
und ![]() nicht beide reell sein. Dasselbe gilt für
nicht beide reell sein. Dasselbe gilt für ![]() und
und ![]()
Lösung:
Im Aufgabentext haben wir den allgemeinen Ansatz für ![]() und
und ![]() , ausgedrückt in der
, ausgedrückt in der ![]() –
–![]() -Basis. Wir wollen nun zeigen, wie weit
-Basis. Wir wollen nun zeigen, wie weit ![]() durch die Produkte mit den anderen Zustandsvektoren bestimmt sind.
durch die Produkte mit den anderen Zustandsvektoren bestimmt sind.
a) Die Produkte mit ![]() und
und ![]() :
:
Es ist nach Gl. 2.8
![]()
![]()
Genau so folgen die Gleichungen
b) Es ist
![]()
Es folgt ![]() , also gilt
, also gilt
![]()
also
![]()
Aus a) wissen wir ![]() , d.h es muss gelten
, d.h es muss gelten
![]()
Mit dem Produkt
c) Aus den Gleichungen in b) folgt, dass ![]() rein imaginär ist, denn es gilt
rein imaginär ist, denn es gilt
![]()
d.h. die konjugiert komplexe Zahl von ![]() ist
ist ![]() .
.
Der Realteil von ![]() ist daher 0, und damit ist
ist daher 0, und damit ist ![]() rein imaginär. Das gleiche gilt für
rein imaginär. Das gleiche gilt für ![]()

Kann es sein, dass sich in die Lösung von 2.3 b) ein Fehler eingeschlichen hat? Wenn man (α*+β*)(α+β) ausmultipliziert, so erhält man meiner Meinung nach α*α+β*β+α*β+αβ*, wie es auch in der vorletzten Zeile des Beweises steht, und nicht α*+α+β*+β+α*β+αβ*, wie es in am Ende der Gleichungskette darüber heißt.
Hallo und vielen Dank für den Hinweis. Ich habe den Fehler korrigiert.
Aufgabe 2.3, b):
Kann es sein, dass |l> = (1/sqrt(2))*( |u> – |d>) ist und nicht |l> = (1/sqrt(2))*( |u> + |d>)?
So steht es zumindest im Buch auf Seite 42 oben.
Hallo Dustin,
stimmt, ich habe hier |l> mit |r> verwechselt, so wie sie in Gl. 2.5 und 2.6 definiert sind. Die Rechnung und Argumentation funktioniert also richtig mit |r>. Das habe ich auch korrigiert. Man beachte aber, dass die Definitionen von |l> und |r> insofern willkürlich sind, als man sie auch „andersherum“ bezeichnen könnte.
Hallo Herr Sippel,
zu Aufgabe 2.2. alle Lösungen hätte ich folgende Anmerkung:
M.E. gehört gemäß Seite 19 Ziffer 2 zum
i-Ket=1/sqrt2 mal u-Ket + i/sqrt2 mal d-Ket
der
i-Bra=u-Bra mal 1/sqrt2 – d-Bra mal i/sqrt2 (also minus statt plus in der Mitte)
und zum
o-Ket=1/sqrt2 mal u-Ket – i/sqrt2 mal d-Ket
der
o-Bra=u-Bra mal 1/sqrt2 + d-Bra mal i/sqrt2 (also plus statt minus in der Mitte),
weil mit Z=i/sqrt2 gilt:
Z-Stern=-i/sqrt2
und umgekehrt.
Dann ergeben sich immer noch die richtigen Lösungen, aber mit einsehbarem Lösungsweg, besonders, was Gleichung 2.7. angeht.
Richtig?
Viele Grüße, Frank Gilewitz
Hallo,
völlig richtig, hier war ich nicht sorgfältig genug. Ich korrigiere das, vielen Dank!