Der zentrale Begriff in den verschiedenen Geometrien ist die Metrik. Durch sie wird es möglich, Abstände zwischen Punkten zu messen, und erst dadurch machen Begriffe wie Geschwindigkeit, Beschleunigung und damit auch Kraft (gemäß der Newtonschen Physik) erst Sinn. In der ART ist der metrische Tensor ein wesentliches Hilfsmittel bei der Untersuchung der Gravitation, da damit die Krümmung des Raums vermessen werden kann.
Der metrische Tensor ist mathematisch gesehen eine quadratische Form, mit der infinitesimal kleine Entfernungen gemessen werden können. Dies sieht in der kompakten Tensorschreibweise mit der Einsteinschen Summenkonvention so aus:
![\[ dS^2 = g_{mn} dX^m dX^n \]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-01fe18e6114dbaeef11886c566fe5ab5_l3.png "Rendered by QuickLaTeX.com")
Dabei sind die 
kurze Abschnitte längs der Koordinatenlinien, und der Ausdruck kann als Verallgemeinerung des Satzes von Pythagoras verstanden werden.
Als quadratische Form kann 
als Matrix geschrieben werden, deren Komponenten von der gewählten Basis abhängt. Die kartesischen Koordinaten haben dabei die Besonderheit, dass die Metrik durch die Einheitsmatrix dargestellt wird, also durch das Kronecker-Delta, und damit in den Berechnung gar nicht erst hingeschrieben wird. Daher haben die meisten in der Schulmathematik nichts von einer Metrik gehört.
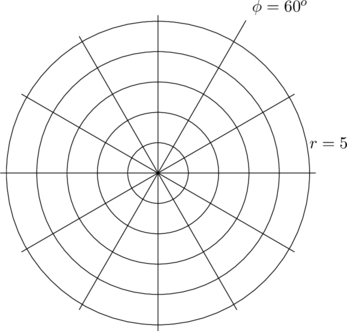
Kartesische Koordinaten haben wir aber nur in flachen Räumen. Andererseits kann man auch auf Ebenen krummlinige Koordinaten einführen, und dies ist auch üblich, wenn sich dadurch Erleichterungen bei Rechnungen ergeben. So sind bei rotationssymmetrischen Problemen Polarkoordinaten sehr praktisch, da sich hierdurch die Zahl der Variablen von 2 auf 1 vermindert, eben die Entfernung zum Ursprung.
Polarkoordinaten
Wir wollen zur Übung einmal den metrischen Tensor berechnen, wenn wir statt kartesischer Koordinaten Polarkoordinaten verwenden. Wir gehen also von den Koordinaten 
über zu 
. Der Zusammenhang zwischen den Koordinaten (die Koordinatentransformation) dürfte vertraut sein:
![\[\begin{split}x &= r \cos \phi\\y &= r \sin \phi\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-b970183fb47357a9f0e7e0e9f6cba783_l3.png "Rendered by QuickLaTeX.com")
![\[\begin{split}r &= \sqrt{x^2 + y^2}\\\phi &= \atan \frac{y}{x}\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-c887c664f52acda5d0fbf586bb46f520_l3.png "Rendered by QuickLaTeX.com")
Wir wollen aus der Formel für die Länge einer kleinen Strecke
![\[ ds^2 = dx^2 + dy^2\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-c756b8752dd41faeab6d251b39edf3dc_l3.png "Rendered by QuickLaTeX.com")
und 
ableiten. Dazu drücken wir 
und 
durch und aus. Es ist
![\[\begin{split}dx &= \pd{x}{r} dr + \pd{x}{\phi}d\phi = \cos\phi\, dr - r \sin\phi\, d\phi,\\ \\dy &= \pd{y}{r} dr + \pd{y}{\phi}d\phi = \sin\phi\, dr + r \cos\phi\, d\phi\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-b69b572f3b32e3745d9df983f49e75ab_l3.png "Rendered by QuickLaTeX.com")
und damit
![\[\begin{split}dx^2 &= \cos^2 \phi\, dr^2 - 2 \sin \phi \cos \phi\, dr d\phi+ r^2 \sin^2 \phi\, d\phi^2,\\ \\dy^2 &= \sin^2 \phi\, dr^2 + 2 \sin \phi \cos \phi\, dr d\phi + r^2 \cos^2 \phi\, d\phi^2\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-b9a263f3fdd083be5e6eaab692993e76_l3.png "Rendered by QuickLaTeX.com")
Es ist also
![\[ds^2 = dx^2 + dy^2 = dr^2 + r^2d\phi^2 \]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-dce7aadd468102107395917a9a8e328c_l3.png "Rendered by QuickLaTeX.com")
da natürlich 
ist und sich die gemischten Terme wegheben.
In Polarkoordinaten ist die Situation also nicht ganz so einfach; der metrische Tensor wird in diesen Koordinaten nicht durch die Einheitsmatrix dargestellt, sondern es ist
![\[g_{r\phi} = \begin{pmatrix}1&0\\0&r^2\end{pmatrix}.\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-b6c0df43dae26ba5cca6e46fb83c133c_l3.png "Rendered by QuickLaTeX.com")
Es ist zwar keine Einheitsmatrix mehr, aber sie ist immerhin noch diagonal. Dies ist immer der Fall, wenn die Koordinatenlinien senkrecht aufeinander stehen, also die beiden „`Richtungen“‚, in denen gemessen wird. Im Fall der Polarkoordinaten stehen die Radien, also die Linien mit konstanten 
, senkrecht auf den Kreisen mit konstantem Wert von 
.
Die Polarkoordinaten sind zwar krummlinig, zumindest die Linien mit 
, aber die Kreise stehen natürlich senkrecht auf den Radien mit 
. Auch das 
ist nicht wirklich überraschend, denn mit größerem Abstand vom Nullpunkt geht mit mehr Gewicht in die Rechnung ein. Verdoppelt sich , so wird auch doppelt so groß nach dem Strahlensatz. Das Maß wächst also nach außen hin linear (die Formel enthält 
, wir müssten also noch die Wurzel ziehen, um die Länge von 
zu erhalten.)
Ist da nicht sin/cos vertauscht? Ich komme auf das hier :
dx = cos(φ)dr – r sin(φ)dφ
dx = sin(φ)dr + r cos(φ) dφ
Das Endergebnis ist dasselbe.
Danke für die Seite & beste Grüße!
Danke für den Hinweis, der Fehler ist korrigiert!
Heiko