Der Übergang von den Lagrange-Gleichungen zu den Hamilton-Gleichungen erscheint weniger rätselhaft, wenn man die mathematische Transformation kennt, durch die diese beiden Darstellungen ineinander überführt werden.
[Einige Teile der Vorlesungen haben es nicht in die Bücher geschafft. Die Legendre-Transformation gehört dazu. Sie ist zum Verständnis der Hamilton-Mechanik nicht notwendig, sie zeigt aber den Weg dahin.]
Wir haben zwei verschiedene Konzepte kennengelernt, aus denen wir die Newtonschen Bewegungsgleichungen ableiten konnten: die Lagrangeschen und die Hamiltonschen Gleichungen. Die Grundlage bilden dabei zwei verschiedene Funktionen; einmal die Lagrange-Funktion ![]() , das andere Mal die Hamilton-Funktion
, das andere Mal die Hamilton-Funktion ![]() . Wir gelangten von der Lagrange-Funktion zur Hamilton-Funktion, indem wir die konjugierten Impulse
. Wir gelangten von der Lagrange-Funktion zur Hamilton-Funktion, indem wir die konjugierten Impulse ![]() einführten und dann
einführten und dann ![]() setzten. Wir haben danach öfter auf die Gleichwertigkeit des Lagrangeschen und Hamiltonschen Ansatzes hingewiesen, aber es scheint doch so zu sein, dass wir die Hamilton-Funktion aus der Lagrange-Funktion ableiten. Die Symmetrie zwischen diesen beiden Funktionen ist aber stärker.
setzten. Wir haben danach öfter auf die Gleichwertigkeit des Lagrangeschen und Hamiltonschen Ansatzes hingewiesen, aber es scheint doch so zu sein, dass wir die Hamilton-Funktion aus der Lagrange-Funktion ableiten. Die Symmetrie zwischen diesen beiden Funktionen ist aber stärker.
Sehen wir uns noch einmal die Ausgangslage an. Die Lagrange-Funktion hängt von den Koordinaten ![]() und den Geschwindigkeiten
und den Geschwindigkeiten ![]() ab, die Hamilton-Funktion dagegen von
ab, die Hamilton-Funktion dagegen von ![]() und den (generalisierten) Impulsen
und den (generalisierten) Impulsen ![]() , was uns dann in den Phasenraum führte. Der Unterschied liegt also darin, dass wir statt der Geschwindigkeiten
, was uns dann in den Phasenraum führte. Der Unterschied liegt also darin, dass wir statt der Geschwindigkeiten ![]() die Impulse
die Impulse ![]() verwenden möchten. Dies ist möglich, da es zwischen den
verwenden möchten. Dies ist möglich, da es zwischen den ![]() und
und ![]() eine ein-eindeutige Beziehung gibt: Aus den Geschwindigkeiten
eine ein-eindeutige Beziehung gibt: Aus den Geschwindigkeiten ![]() folgen die Werte für die Impulse
folgen die Werte für die Impulse ![]() , und umgekehrt. Wir haben damit eine Funktion vorliegen, die die
, und umgekehrt. Wir haben damit eine Funktion vorliegen, die die ![]() auf die
auf die ![]() abbildet, und umgekehrt die
abbildet, und umgekehrt die ![]() auf die
auf die ![]() . Dies können wir uns grafisch so vorstellen wie in der folgenden Abbildung:
. Dies können wir uns grafisch so vorstellen wie in der folgenden Abbildung:
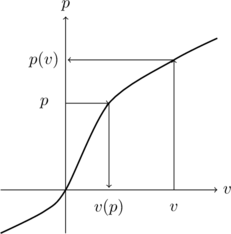
Wir haben hier eine spezielle Funktion abgebildet, die stetig wächst. Wir hätten auch eine stetig fallende Kurve zeichnen können. Wichtig ist aber, dass man von einem ![]() immer zu einem
immer zu einem ![]() gelangt, und umgekehrt. Als weitere Vereinfachung nehmen wir auch an, dass die Kurve durch den Nullpunkt verläuft. Dies stellt keine wesentliche Einschränkung dar, wie wir noch sehen werden.
gelangt, und umgekehrt. Als weitere Vereinfachung nehmen wir auch an, dass die Kurve durch den Nullpunkt verläuft. Dies stellt keine wesentliche Einschränkung dar, wie wir noch sehen werden.
Wir geben der Funktion auch gar keinen speziellen Namen, sondern stellen einfach fest, dass die Impulse ![]() Funktionen der Geschwindigkeiten
Funktionen der Geschwindigkeiten ![]() sind, und umgekehrt die Geschwindigkeiten
sind, und umgekehrt die Geschwindigkeiten ![]() Funktionen der Impulse
Funktionen der Impulse ![]() :
:
(1) ![]()
Vergessen wir für einen Moment, dass es sich bei ![]() und
und ![]() um physikalische Größen handelt; wir könnten sie auch mit mit den Variablen-Namen
um physikalische Größen handelt; wir könnten sie auch mit mit den Variablen-Namen ![]() und
und ![]() bezeichnen. Das folgende gilt tatsächlich immer dann, wenn wir eine eineindeutige Abbildung haben.
bezeichnen. Das folgende gilt tatsächlich immer dann, wenn wir eine eineindeutige Abbildung haben.
Wann immer die beiden Gleichungen 1 erfüllt sind, so gibt es eine Funktion ![]() mit
mit
(2) ![]()
Umgekehrt gibt es auch eine Funktion ![]() mit
mit
![]()
Wir könnten die Funktionen ![]() und
und ![]() auch mit
auch mit ![]() und
und ![]() bezeichnen, denn dies gilt unabhängig von irgendwelchen physikalischen Realitäten. Wir verwenden aber weiterhin
bezeichnen, denn dies gilt unabhängig von irgendwelchen physikalischen Realitäten. Wir verwenden aber weiterhin ![]() und
und ![]() , um den Überblick zu behalten. Dafür lassen wir der Einfachheit halber die Variable der Koordinaten
, um den Überblick zu behalten. Dafür lassen wir der Einfachheit halber die Variable der Koordinaten ![]() weg.
weg.
Um die Existenz von ![]() und
und ![]() einzusehen, setzen wir einfach
einzusehen, setzen wir einfach
(3) 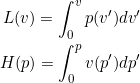
Dies sind die bestimmten Integrale der Funktionen ![]() bzw.
bzw. ![]() . Der Hauptsatz der Differential- und Integralrechnung besagt nun, dass
. Der Hauptsatz der Differential- und Integralrechnung besagt nun, dass
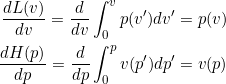
gilt, d.h. ![]() und
und ![]() erfüllen genau die Bedingungen der Gleichungen (1) und (2). Hier sehen wir auch, dass wir unsere Funktion der Einfachheit halber durch den Nullpunkt gehen lassen konnten; eine Verschiebung nach oben oder unten hätte nur Konstanten erzeugt, die sich dann weggekürzt hätten.
erfüllen genau die Bedingungen der Gleichungen (1) und (2). Hier sehen wir auch, dass wir unsere Funktion der Einfachheit halber durch den Nullpunkt gehen lassen konnten; eine Verschiebung nach oben oder unten hätte nur Konstanten erzeugt, die sich dann weggekürzt hätten.
![]() und
und ![]() sind also gerade die Flächen rechts unterhalb bzw. links oberhalb des Funktionsgraphen:
sind also gerade die Flächen rechts unterhalb bzw. links oberhalb des Funktionsgraphen:
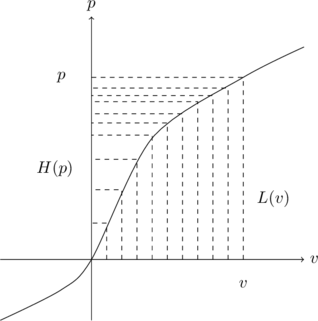
Zusammen ergeben sie die Fläche des Rechtecks, das durch ![]() und
und ![]() erzeugt wird:
erzeugt wird:
![]()
In dieser Gleichung sind ![]() und
und ![]() auf der linken Seite und
auf der linken Seite und ![]() und
und ![]() völlig gleichwertig.
völlig gleichwertig.
Gehen wir nun von ![]() zu
zu ![]() über, so erhalten wir
über, so erhalten wir
![]()
Dies ist genau die Definition der Hamilton-Funktion. Es gilt aber auch umgekehrt:
![]()
d.h. die Lagrange-Funktion ergibt sich auf völlig symmetrische Weise aus der Hamilton-Funktion.
Dieser allgemeingültige Übergang von ![]() zu
zu ![]() und von
und von ![]() nach
nach ![]() wird in der Mathematik Legendre-Transformation genannt. Sie ist immer dann möglich, wenn zwischen zwei Variablen
wird in der Mathematik Legendre-Transformation genannt. Sie ist immer dann möglich, wenn zwischen zwei Variablen ![]() und
und ![]() eine ein-eindeutige Beziehung besteht und man die Variable
eine ein-eindeutige Beziehung besteht und man die Variable ![]() durch
durch ![]() ersetzen möchte.
ersetzen möchte.
Wir sehen also, dass durch die Legendre-Transformation und dem Übergang von ![]() zu
zu ![]() die Hamilton-Funktion aus der Lagrange-Funktion entsteht. Dieser Übergang ist auch umgekehrt möglich, falls man mit den generalisierten Koordinaten beginnt. Während wir mit den Geschwindigkeiten
die Hamilton-Funktion aus der Lagrange-Funktion entsteht. Dieser Übergang ist auch umgekehrt möglich, falls man mit den generalisierten Koordinaten beginnt. Während wir mit den Geschwindigkeiten ![]() eine konkrete Vorstellung verbinden, sind die generalisierten Impulse
eine konkrete Vorstellung verbinden, sind die generalisierten Impulse ![]() abstrakter und entziehen sich mitunter der Vorstellung. Dafür haben wir festgestellt, dass
abstrakter und entziehen sich mitunter der Vorstellung. Dafür haben wir festgestellt, dass ![]() die Energie des Systems beschreibt, während die Lagrange-Funktion
die Energie des Systems beschreibt, während die Lagrange-Funktion ![]() keine für uns wahrnehmbare und meßbare Größe darstellt. Ansonsten sind die Ansätze aber gleichwertig, denn bei dem Übergang haben wir lediglich geometrische Einsichten verwendet und keine physikalischen.
keine für uns wahrnehmbare und meßbare Größe darstellt. Ansonsten sind die Ansätze aber gleichwertig, denn bei dem Übergang haben wir lediglich geometrische Einsichten verwendet und keine physikalischen.

