Wir haben in der Klassischen Mechanik gesehen, wie aus dem Prinzip der kleinsten Wirkung die Newtonschen Gesetze abgeleitet werden können. Die Prinzipien sind fundamentaler, die Gesetze aber näher an unserer Realität und Wahrnehmung, intuitiver. Mit ihnen lässt sich oft leichter rechnen, und sie standen immer an Anfang der Entwicklung. Wir haben auch die Drehimpulserhaltung kennengelernt, und dieses aus dem Noether-Theorem abgeleitet, indem wir den Raum als isotrop voraussetzten, also in jeder richtig „gleich“. Wir können so zwar sagen, dass ein Kreisel eben nicht einfach umkippt, aber können wir auch die Kräfte erklären, die ja wirken müssen, damit das Prinzip gültig bleibt?
Das Fermatsche Prinzip
In diesem Artikel möchte ich zeigen, wie man aus dem Fermatschen Prinzip das Snelliussche Gesetz herleiten kann. Das Fermatsche Prinzip besagt vereinfacht:
Das Licht nimmt den Weg mit der kürzesten Laufzeit.
Das ist sehr knapp formuliert. Was bedeutet das eigentlich? Wenn ein Lichtstrahl von einem Punkt ![]() zu einem Punkt
zu einem Punkt ![]() geht, so läuft er einen Weg entlang, der in dem Sinne optimal ist, als dass er auf jedem anderen Weg eine längere Laufzeit benötigt. Aber ist das nicht immer die Strecke, also der kürzeste Weg, zwischen diesen beiden Punkten? Deshalb spricht man doch auch von Lichtstrahlen. Das ist natürlich richtig, gilt aber nur, wenn das Licht sich immer im selben Medium fortbewegt, etwa im Vakuum, in der Luft oder in Wasser.
geht, so läuft er einen Weg entlang, der in dem Sinne optimal ist, als dass er auf jedem anderen Weg eine längere Laufzeit benötigt. Aber ist das nicht immer die Strecke, also der kürzeste Weg, zwischen diesen beiden Punkten? Deshalb spricht man doch auch von Lichtstrahlen. Das ist natürlich richtig, gilt aber nur, wenn das Licht sich immer im selben Medium fortbewegt, etwa im Vakuum, in der Luft oder in Wasser.
Was zeichnet die unterschiedlichen Medien aus? Das Licht hat in verschiedenen Medien verschiedene Geschwindigkeiten, und die berühmte Konstante ![]() ist eben die Lichtgeschwindigkeit im Vakuum, obwohl dies nicht immer explizit gesagt wird. In anderen materiegefüllten Medien ist die Lichtgeschwindigkeit niedriger wegen der Wechselwirkung des Lichts mit der Materie. Dies macht sich genau dann bemerkbar, wenn das Licht von einem Medium in ein anderes übertritt. Dann kommt es zu den bekannten Brechungseffekten.
ist eben die Lichtgeschwindigkeit im Vakuum, obwohl dies nicht immer explizit gesagt wird. In anderen materiegefüllten Medien ist die Lichtgeschwindigkeit niedriger wegen der Wechselwirkung des Lichts mit der Materie. Dies macht sich genau dann bemerkbar, wenn das Licht von einem Medium in ein anderes übertritt. Dann kommt es zu den bekannten Brechungseffekten.
Welcher Weg ist der schnellste?
Dem Licht bleibt nach dem Fermatschen Prinzip nichts anderes übrig, als in der der kürzesten Zeit (noch einmal: nicht unbedingt auf dem kürzesten Weg) von ![]() nach
nach ![]() zu gelangen. Wir Menschen sind dagegen frei in der Wahl unseres Weges, und wer öfters mit dem Taxi fährt, kennt die Frage: „Den kürzesten oder den schnellsten Weg?“ Der schnellste Weg ist dann meist ein Umweg, der aber vielleicht über die Autobahn geht, wo man einige Zeit schneller unterwegs ist.
zu gelangen. Wir Menschen sind dagegen frei in der Wahl unseres Weges, und wer öfters mit dem Taxi fährt, kennt die Frage: „Den kürzesten oder den schnellsten Weg?“ Der schnellste Weg ist dann meist ein Umweg, der aber vielleicht über die Autobahn geht, wo man einige Zeit schneller unterwegs ist.
Ein weiteres bekanntes Beispiel: Wir sind an einem schönen Sandstrand am Punkt ![]() und sehen jemandem im Punkt
und sehen jemandem im Punkt ![]() im Wasser, der uns zuwinkt. Wie kommen wir am schnellsten dahin? Der kürzeste Weg ist sicher die Gerade (rote Linie):
im Wasser, der uns zuwinkt. Wie kommen wir am schnellsten dahin? Der kürzeste Weg ist sicher die Gerade (rote Linie):
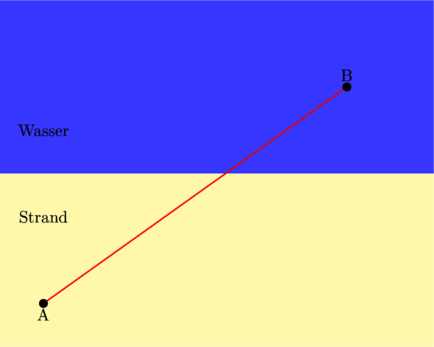
Aber das bedeutet, dass wir auch ein gutes Stück des Weges im Wasser zurücklegen müssen, und wir laufen sicher sehr viel schneller, als wir schwimmen können. Es ist daher geschickter, etwas weiter nach rechts zu laufen, um dann nicht so weit schwimmen zu müssen, vielleicht sogar, bis wir mit dem Schwimmer auf einer Höhe sind (blaue Verbindung). Aber das ist dann schon ein ziemlicher Umweg. Wahrscheinlich ist ein Kompromiss zwischen diesen beiden Möglichkeiten ideal (gestrichelte Linie):

Es ist klar, dass die Wege auf dem Strand und im Wasser gerade Linien sind, denn sie sind ja die kürzesten Verbindungen. Beim Übergang vom Strand ins Wasser entsteht dadurch ein Knick.
Das Gesetz von Snellius
Dasselbe gilt für einen Lichtstrahl, der einen Teil des Weges durch die Luft zurücklegt und danach in Wasser eindringt. Auch bei ihm entsteht ein Knick, was eigentlich ziemlich merkwürdig ist. Aber wir kennen den Grund: das Fermatsche Prinzip.
Können wir mit diesem Wissen den genauen Lichtweg berechnen? Ja, das ist möglich, wenn wir die Lichtgeschwindigkeit in den beiden Medien kennen. Es geht dann nur noch darum, die Stelle ![]() zu finden, an die der Lichtstrahl ins Wasser eindringt. Dasselbe gilt für uns, wenn wir den optimalen Weg zum Schwimmer suchen. Machen wir eine neue Skizze:
zu finden, an die der Lichtstrahl ins Wasser eindringt. Dasselbe gilt für uns, wenn wir den optimalen Weg zum Schwimmer suchen. Machen wir eine neue Skizze:
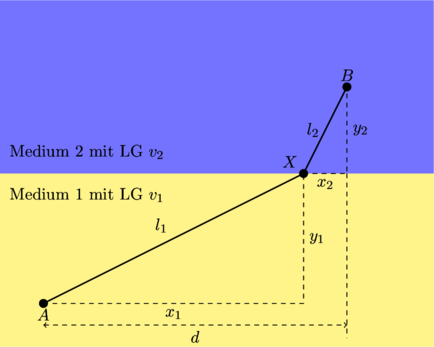
Mal sehen, was wir da haben. Von ![]() geht ein Lichtstrahl aus, der sich durch das Medium 1 mit Geschwindigkeit
geht ein Lichtstrahl aus, der sich durch das Medium 1 mit Geschwindigkeit ![]() bewegt und im Übergangs-Punkt
bewegt und im Übergangs-Punkt ![]() in das Medium 2 eintritt, wo er sich mit der Geschwindigkeit
in das Medium 2 eintritt, wo er sich mit der Geschwindigkeit ![]() bis zum Punkt
bis zum Punkt ![]() bewegt.
bewegt.
Die Länge der beiden zurückgelegten Teilstrecken ![]() und
und ![]() nenne ich
nenne ich ![]() und
und ![]() . Die ergeben sich aus den gestrichelten Dreiecken nach dem Satz von Pythagoras zu
. Die ergeben sich aus den gestrichelten Dreiecken nach dem Satz von Pythagoras zu
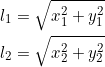
Der Punkt ![]() ist nun durch z.B. die Länge
ist nun durch z.B. die Länge ![]() eindeutig bestimmt. Die Laufzeit des Lichts
eindeutig bestimmt. Die Laufzeit des Lichts ![]() längs des Wegs
längs des Wegs ![]() ist also eine Funktion von
ist also eine Funktion von ![]() , wenn ich
, wenn ich ![]() durch
durch ![]() ersetze, wobei
ersetze, wobei ![]() der horizontale Abstand von
der horizontale Abstand von ![]() und
und ![]() ist:
ist:
![]()
Um den kürzesten Weg zu finden, berechne ich das Minimum von
![]()
Wenn ich das auf den Hauptnenner bringe, brauche ich nur den Zähler zu behalten, weil das ganze 0 ergeben soll:
![]()
Wenn ich jetzt ![]() wieder durch
wieder durch ![]() ersetze, kann ich es so umformen:
ersetze, kann ich es so umformen:
![]()
Setzen wir für die Ausdrücke in den Wurzeln wieder die Längen ein:
![]()
Immerhin ein hübsch symmetrischer Ausdruck. Machen wir weiter:
![]()
Aha! Jetzt haben wir hier einige Längenverhältnisse in rechtwinkligen Dreiecken. Ich trage mal ein paar Winkel ein.
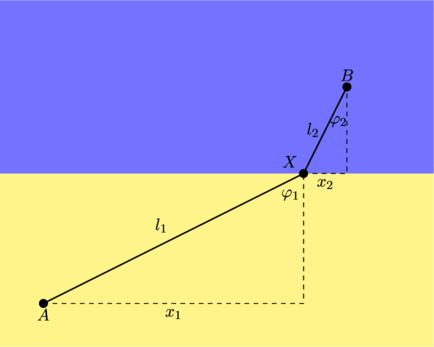
Offenbar ist
![Rendered by QuickLaTeX.com \[\begin{split}\sin \varphi_1 &= \frac{x_1}{l_1}\\\sin \varphi_2 &= \frac{x_2}{l_2}\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-9a9752bee618ce579d9553aa848b7a52_l3.png)
Damit gilt also
![]()
Die beiden Geschwindigkeiten verhalten sich also wie die beiden Winkel.
Das ist genau das Snelliussche Gesetz, das man schon auf der Schule lernt (und älter als das Fermatsche Prinzip ist):
![]()
und
Für Luft und Wasser wären das also etwa:
![Rendered by QuickLaTeX.com \[\begin{split}n_{Luft} = \frac{v_{Luft}}{c} = 1,0009\\n_{Wasser} = \frac{v_{Wasser}}{c} = 1,33\end{split}\]](https://www.das-theoretische-minimum.de/wp-content/ql-cache/quicklatex.com-0823918601439bd83a207c91b48c5235_l3.png)
Und wenn wir mit 15 km/h den Strand entlanglaufen, aber nur mit 5 km/h schwimmen, so wäre der Brechungsindex etwa 3.

